CLOTH SIMULATOR

OVERVIEW

In this project, I implemented a three-dimensional cloth simulator using a grid of springs and point masses. In generating this grid, I enforced several constraints to create a realistic model. These include structural, shearing, and bending constraints. Next I applied external forces, like gravity, on the springs, and used Hooke's law to accumulate the forces added by the springs. The point mass positions were then updated using Verlet integration. This generated a fairly realistic approximation of the motion of cloth as it falls. I also implemented collisions with other objects, like spheres and planes, by correcting certain point mass positions. Finally, I implemented self-collisions by paritioning the 3D space into 3D boxes and using a hash table to map these boxes to the relevant point masses. If two point masses in a box are too close, their positions are corrected. Self-collisions allow the cloth to properly fold over itself, as opposed to falling through itself.

PART 1: MASSES AND SPRINGS

We first need to create a grid of point masses and springs to represent the cloth model. We create evenly spaced point masses over the height and width of the cloth, depending on num_width_points and num_height_points. The distance between points would then be given by width / num_width_points and height / num_height_points. If the cloth's orientation is horizontal, we vary positions over the xz plane and set y to 1. If the orientation is vertical, we vary positions over the xy plane and set z to a random offset between -1/1000 and 1/1000. If the point mass is in the pinned vector, we mark it as pinned. Next, we will use springs to enforce certain constraints. Structural springs exist between a point mass and the point mass to its left as well as the one above it. These enforce the cloth's grid structure. Shearing constraints exist between a point mass and the point mass to its diagonal upper left as well as the one to its diagonal upper right. These, as the name suggests, prevent the cloth from shearing. Bending constraints exist between a point mass and the point mass two away to its left as well as the one two above it. These prevent too much bending in the third dimension. Once the springs have been added, we can see a wireframe in the GUI, as pictured below.

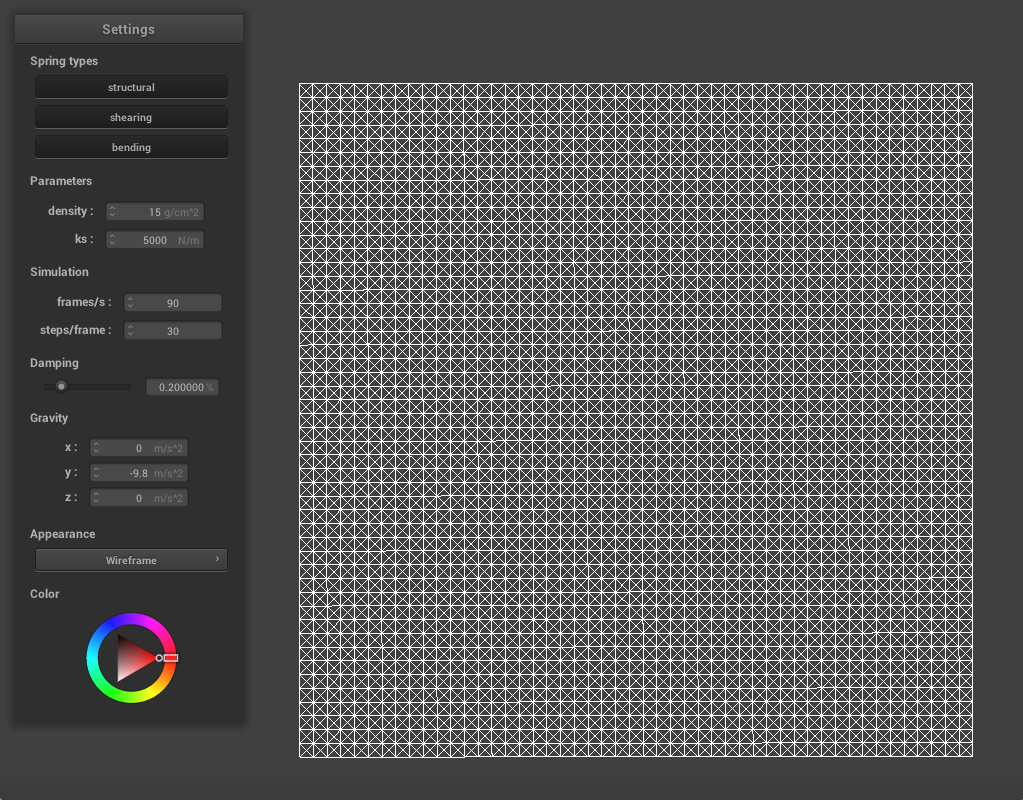
The shearing springs are along the diagonal while the structural and bending springs create a grid, as shown below.

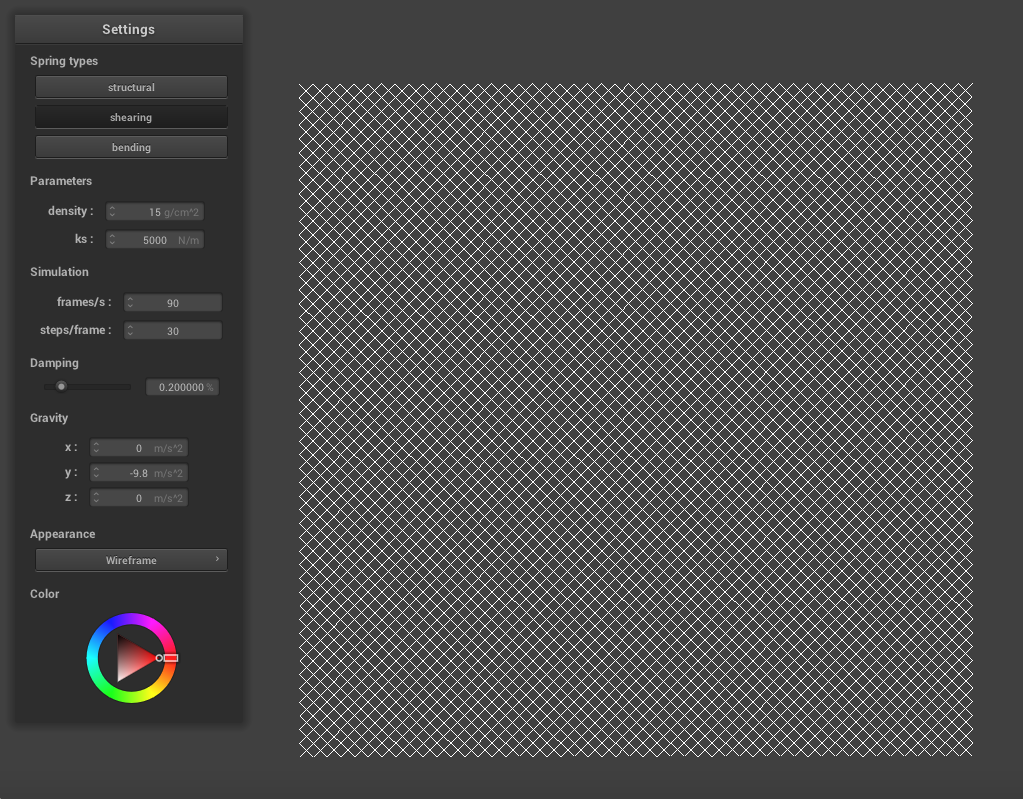
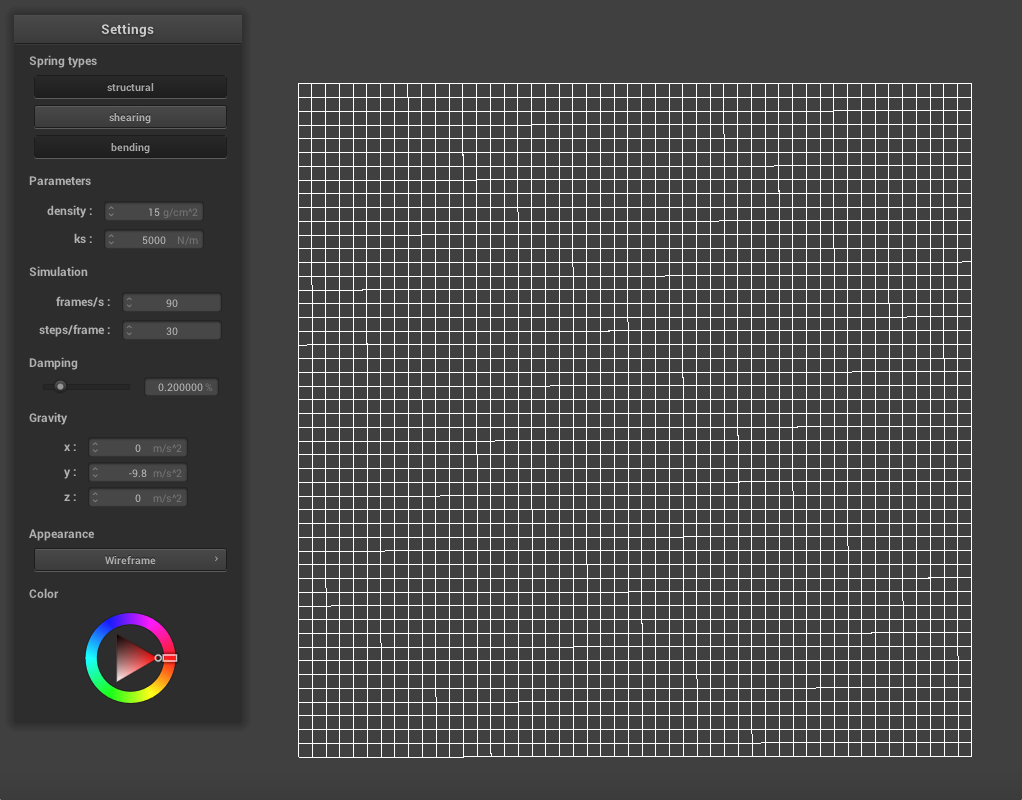
PART 2: SIMULATION

In this part, we simulate the motion of cloth. First, we accumulate all of the external forces on the cloth, like gravity. Next we need to apply the spring correction forces. For each spring, we can calculate the force applied to the two masses on its ends using Hooke's law:

Fs = ks * (||pos_a - pos_b|| - rest_length)

Bending contraints are weaker than structural or shearing. We apply the ||Fs|| to one point mass and -||Fs|| to the other. Next we use Verlet integration to compute the new position of each point mass. This new position is calculated as

x_(t + d_t) = x_t + (1 − damping) * (x_t − x_(t − d_t) + a_t * (d_t)^2

where a_t is calculated using the mass and the force vector of the point mass. We only adjust the position of point masses that are not pinned. Finally, we constrain these position updates so that a spring is never stretched more than 110% of its resting length. This generates a more realistic final result by preventing over-deformation of the springs. Here is the final result with the top two corners pinned, at default settings (ks = 5000, density = 1.5, damping = 0.2).

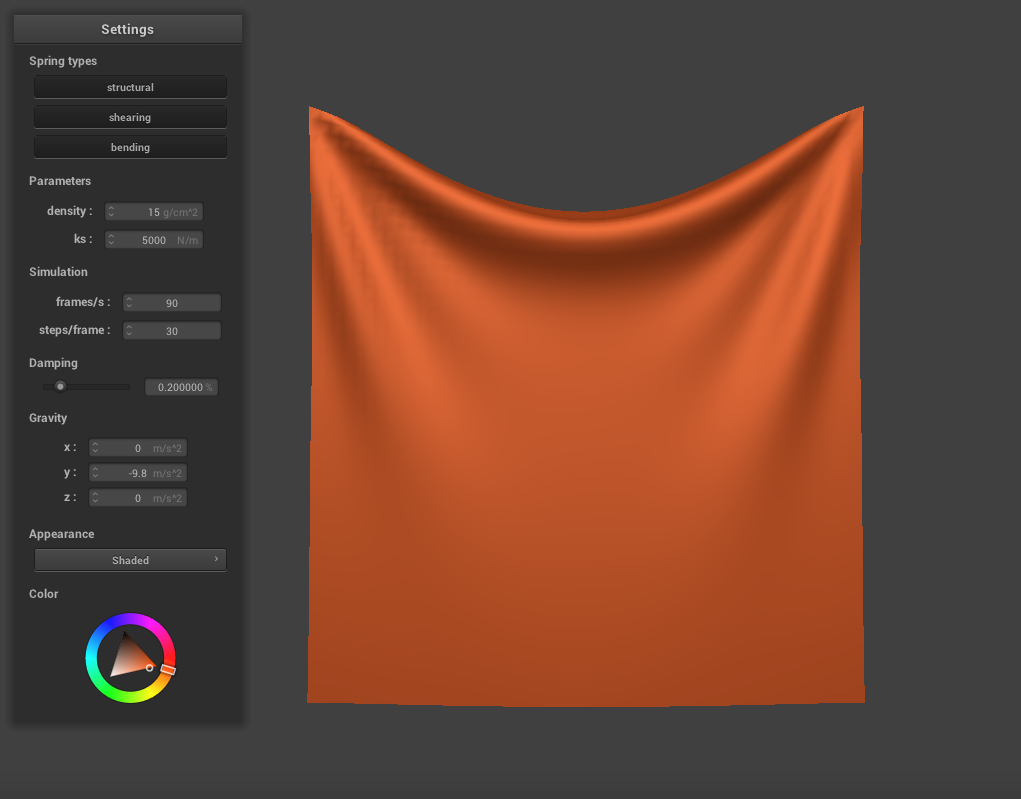
Varying the Spring Constant

We can change the spring constant ks to alter the appearance of the cloth. When we decrease ks to 1000, the cloth appears to be thinner and stretchier as it falls, folding more easily. The cloth deforms more and appears more sunken in the center. When we increase ks to 20000, the cloth appears much stiffer and thicker. It is more resistant to deformation overall and sinks less in the center.

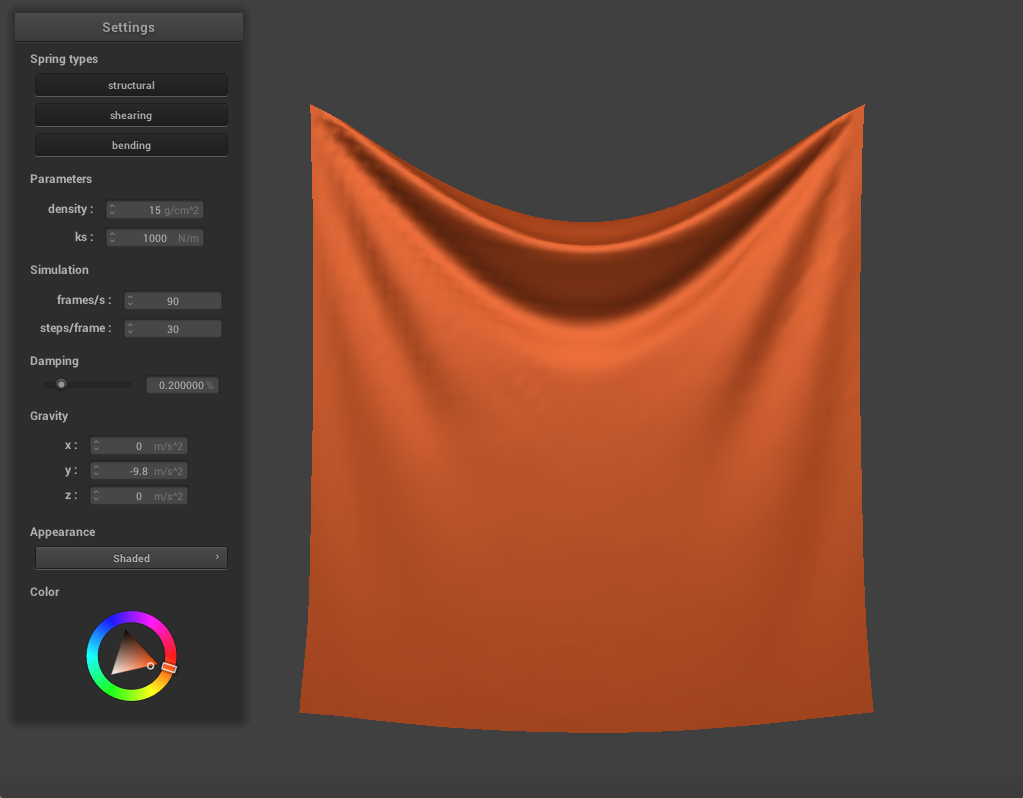
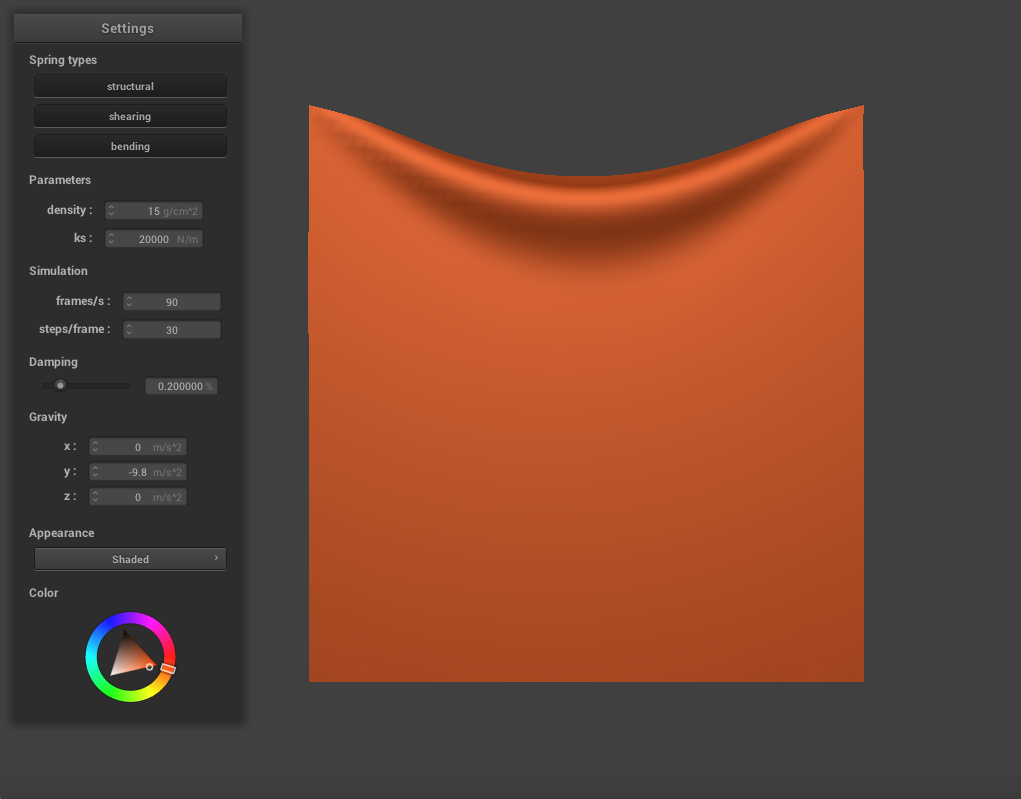
Varying the Density

Similarly, we can also change the density to alter the cloth's properties. Decreasing the density to 1.5 produces a much heavier and stiffer cloth. In it's final resting state, there is only a slight deformation and it sinks very little in the center. When we increase the density to 100, a much thinner and lighter cloth is produced. The cloth creases very easily, and these creases ripple through it as it falls.

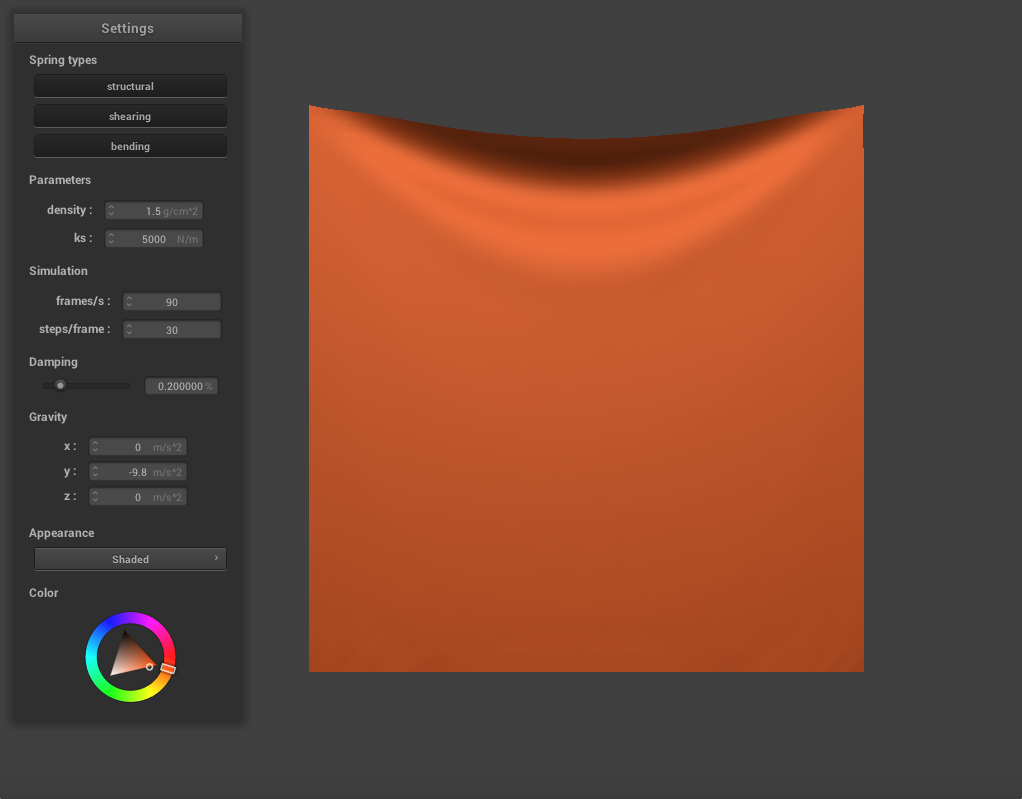
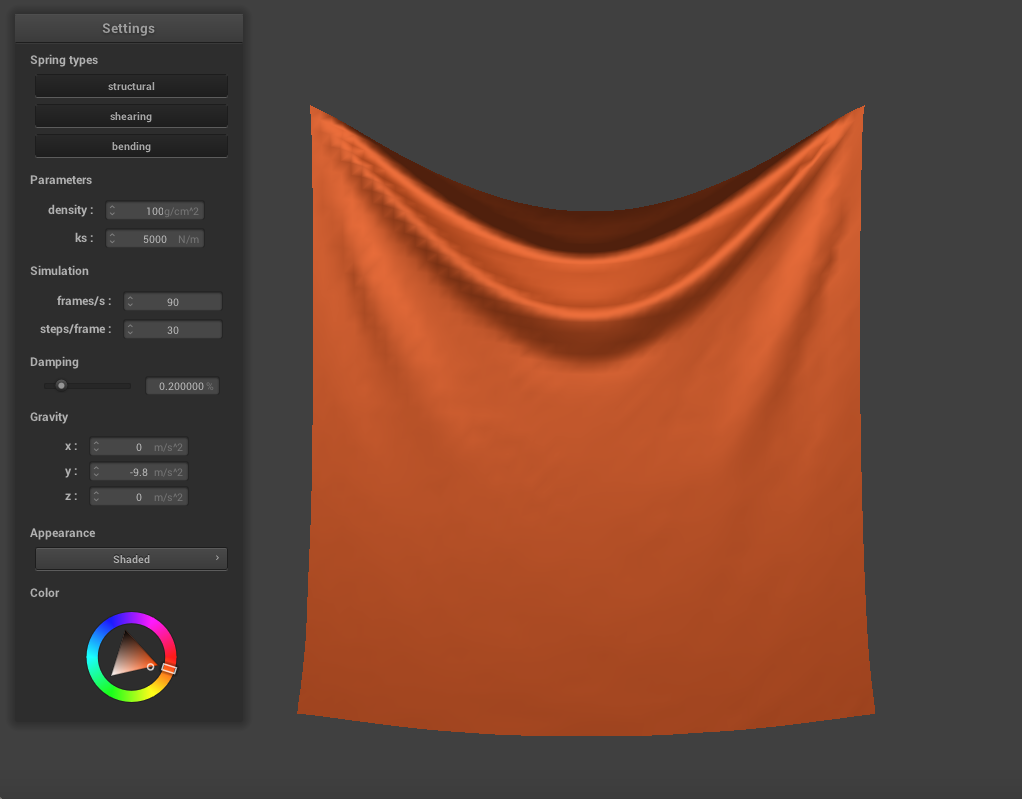
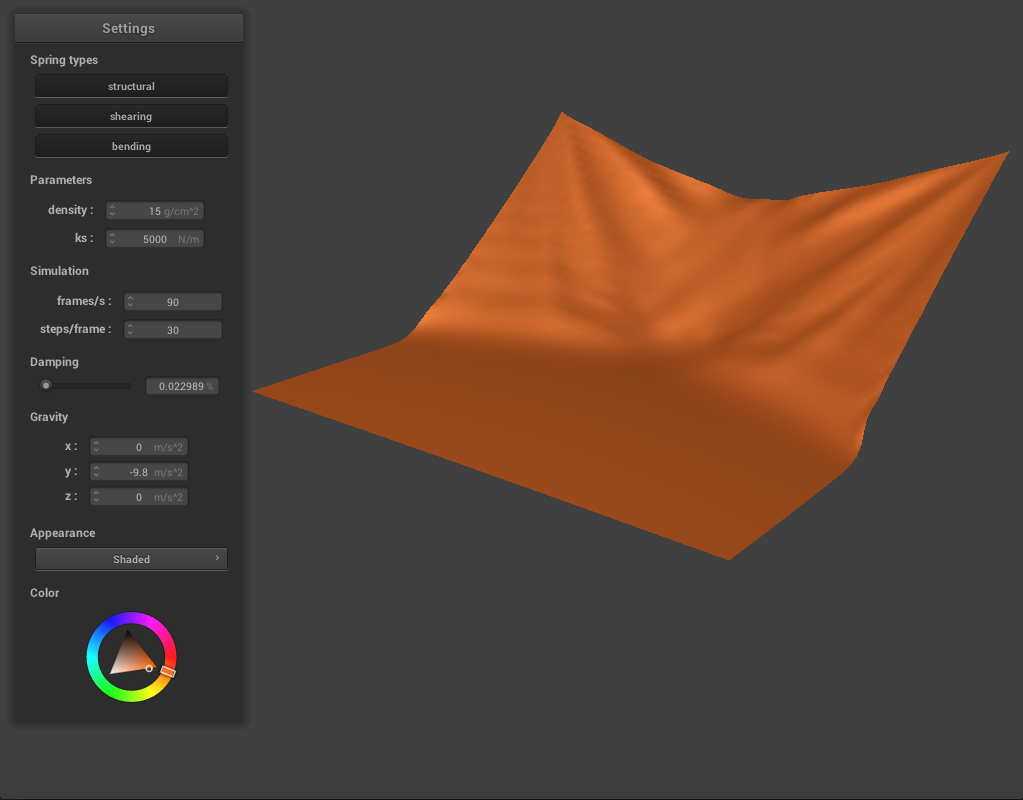
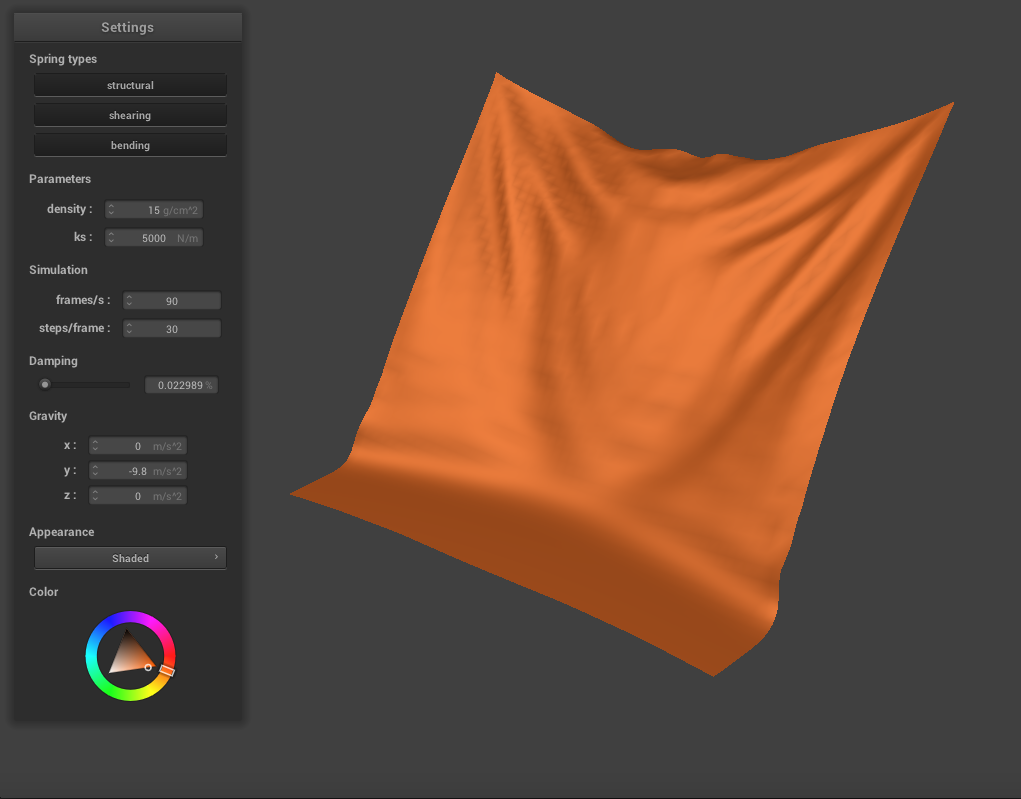
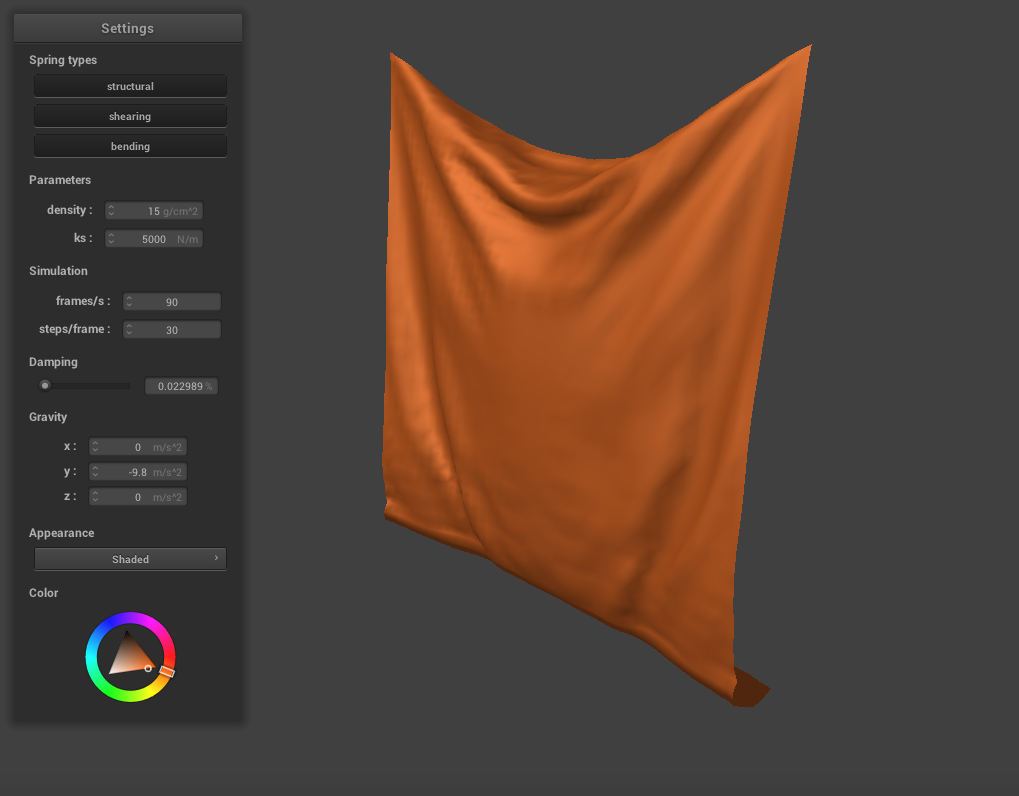
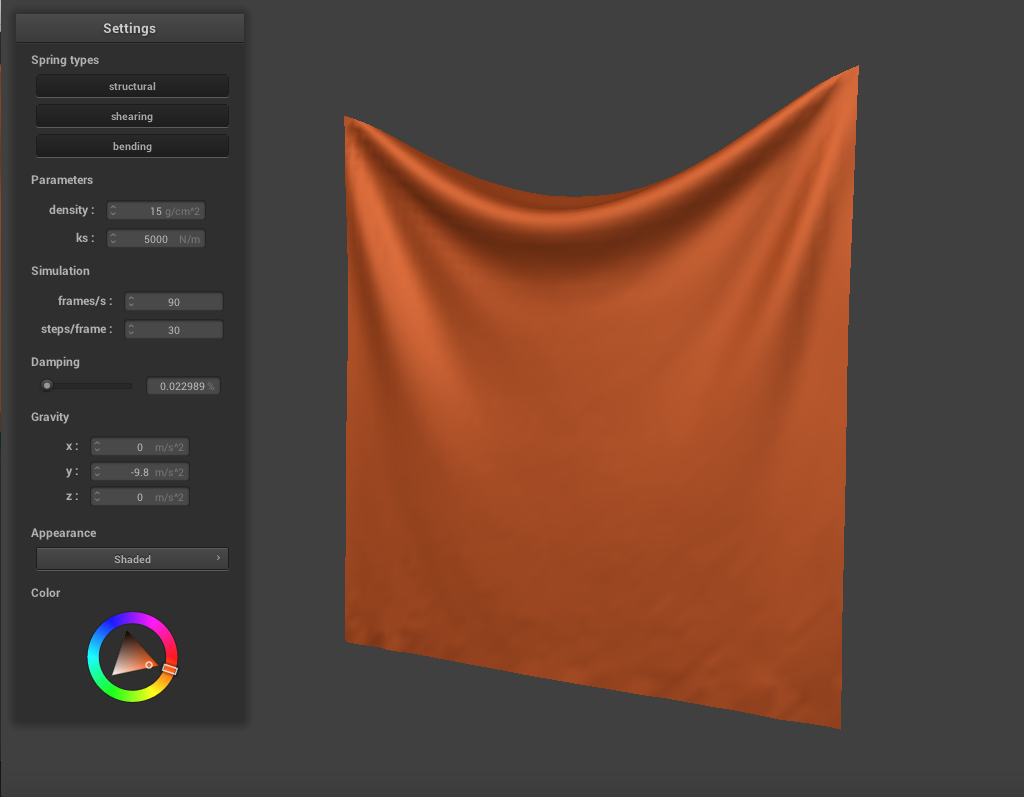
Varying the Damping Constant

We can also vary the damping constant to change how the cloth falls. When we lower it to around 0.1, the range of motion as the cloth falls becomes more exaggerated, as expected. There are more creases and rippling as the cloth falls, and it swings back past its resting position before finally coming to a stop.

When we increase the damping constant to around 0.9, the cloth seems much stiffer and falls very slowly and gradually. There are very few creases and essentially no rippling, and the cloth never swings past it's resting point.

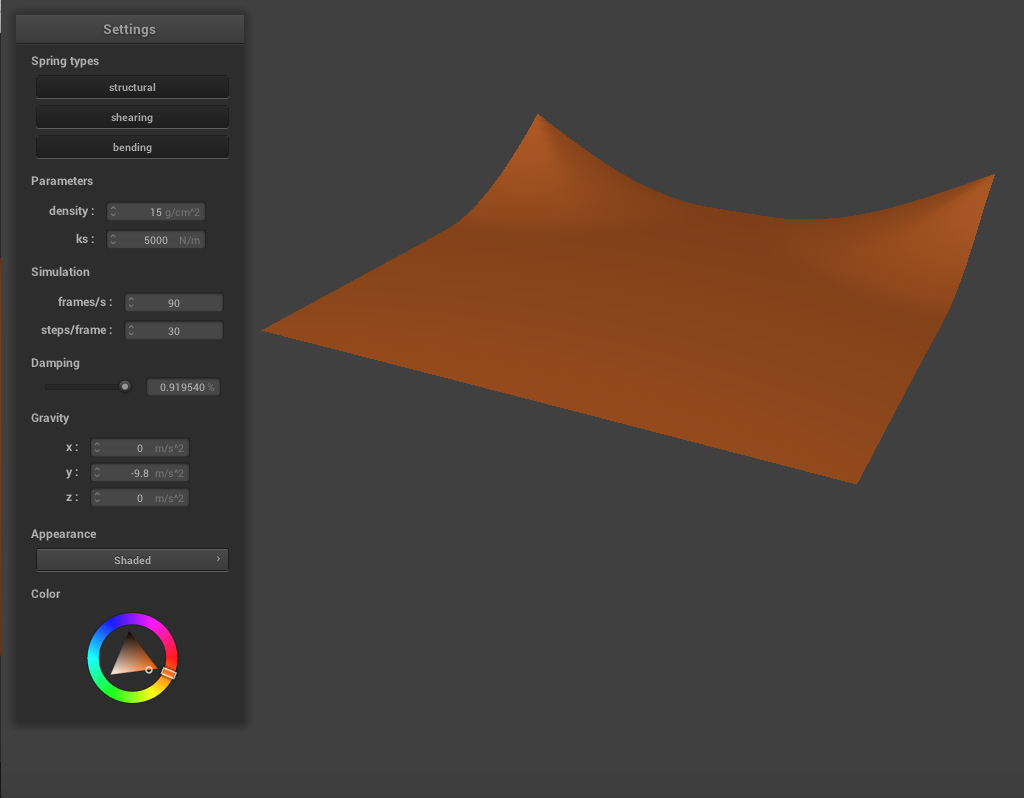
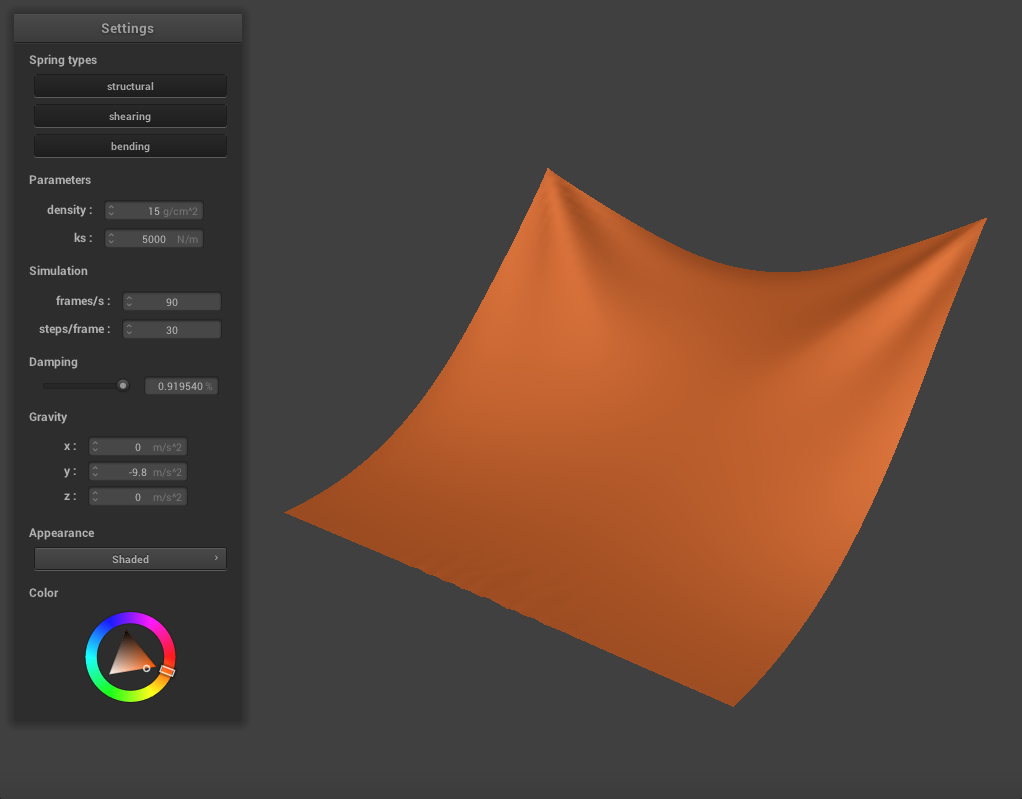
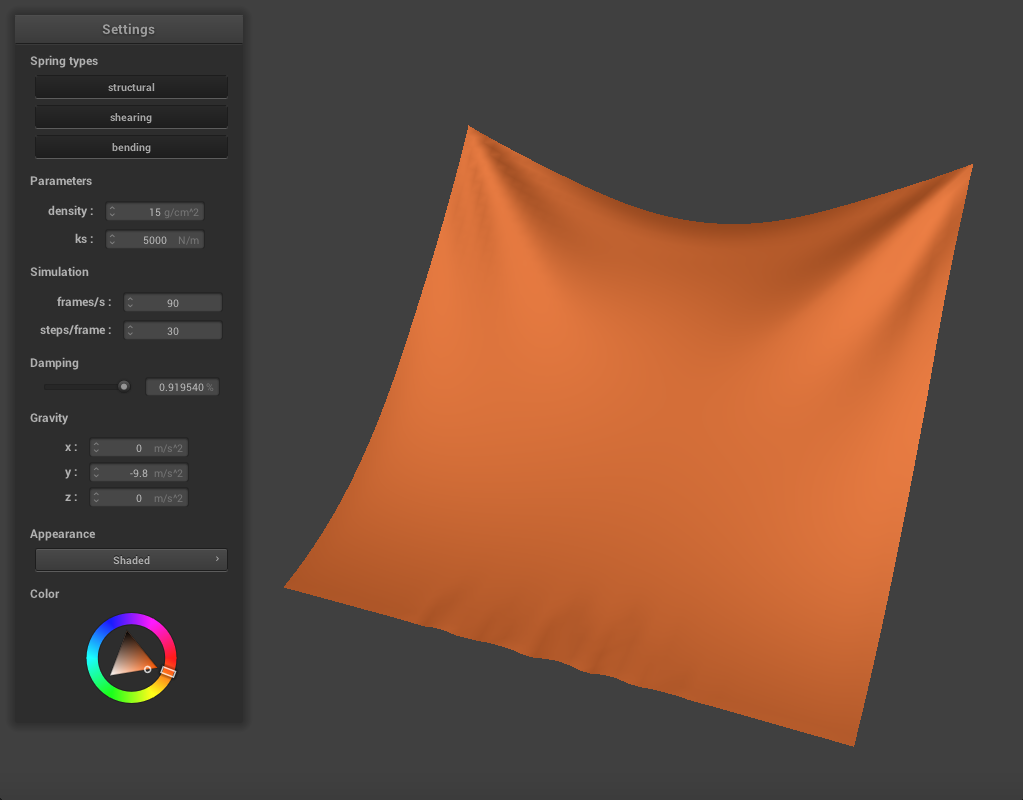
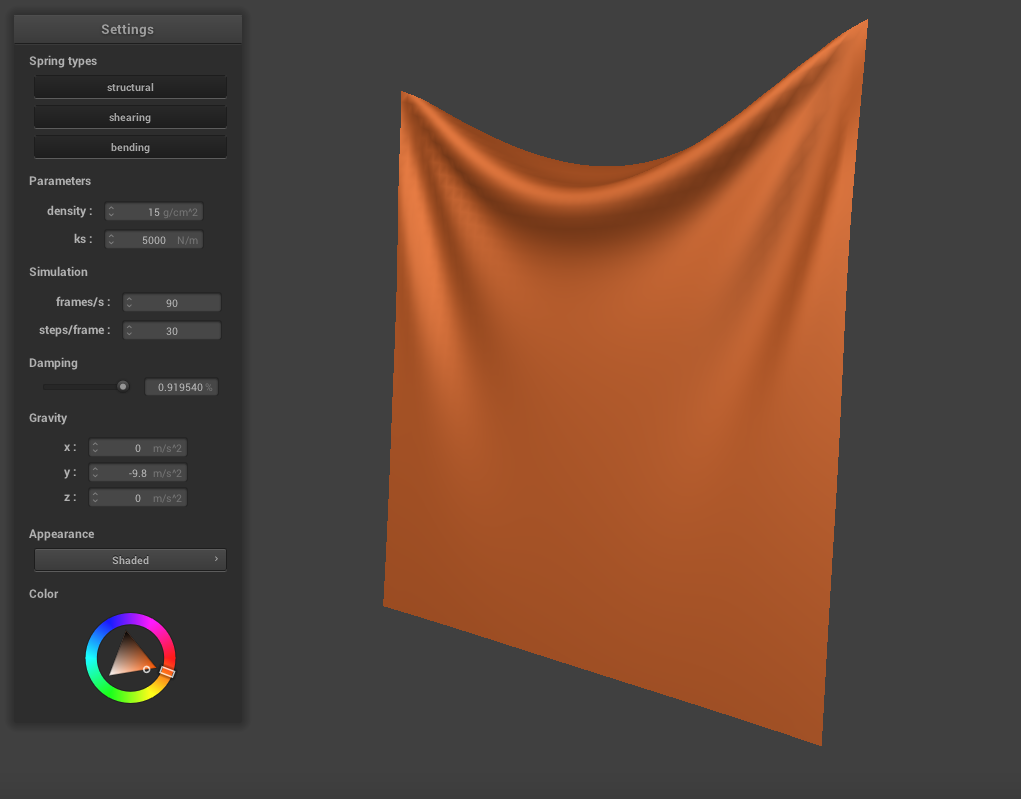
PART 3: COLLISIONS WITH OTHER OBJECTS

In this section, we will handle collisions with spheres and planes. To do so, we check whether a point mass has collided with the object. For spheres, this means checking if the point mass intersects with is or inside the sphere. For planes, this means checking if the point mass crosses over to the far side of the plane. If the point collides, we calculate where it should have intersected the sphere, by adjusting the position along the vector. This new position, the tangent point, is used to calculate a correction vector from the last position. We then set the point mass's position to be it's last position, adjusted by (correction_vector * (1 - friction)). For plane intersections, we use a surface offset to make sure the point appears on the correct side of the plane.

Sphere collision

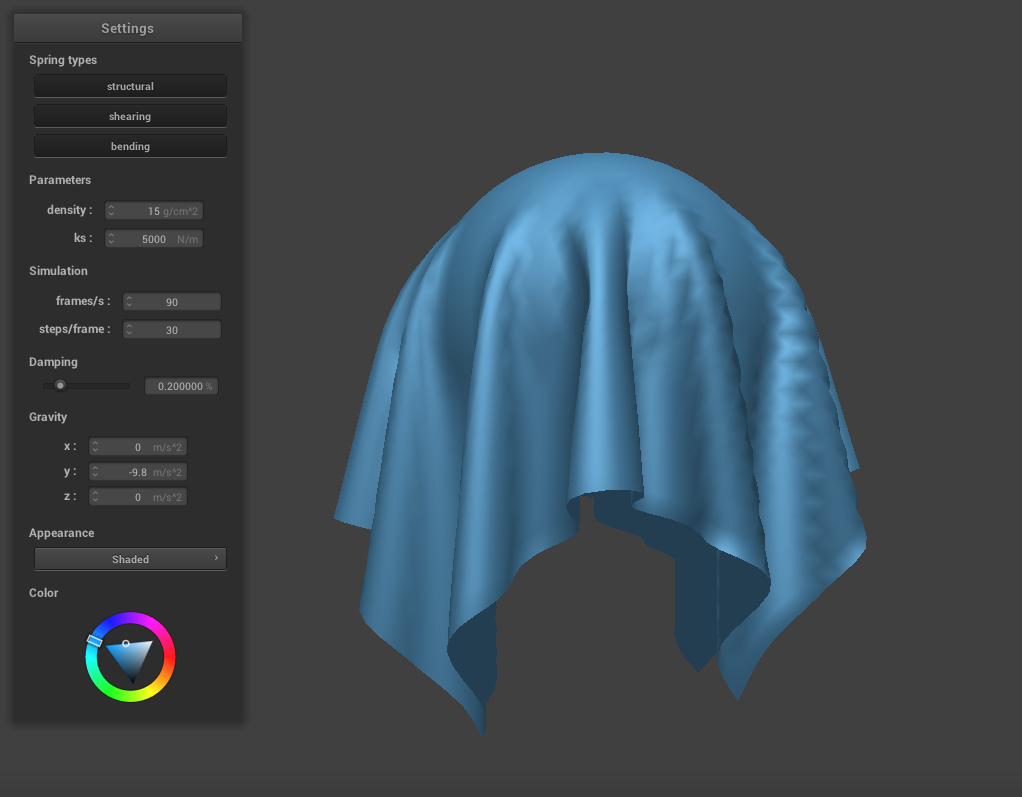
The image below demonstrates a sphere collision with ks = 5000.

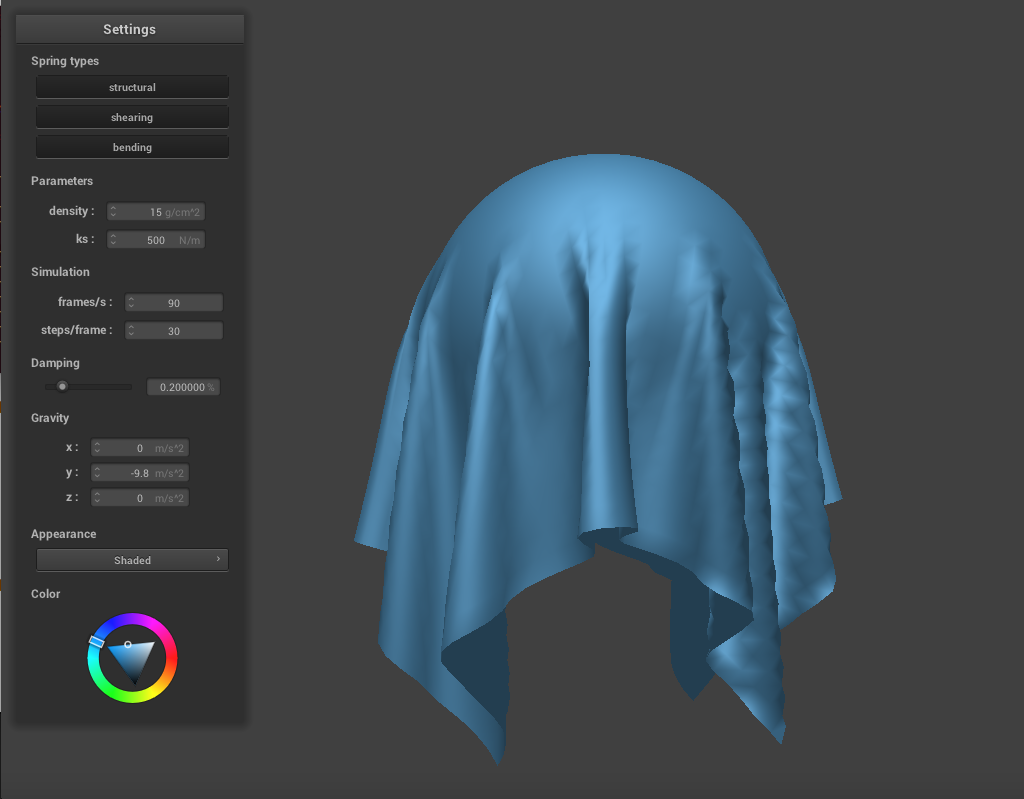
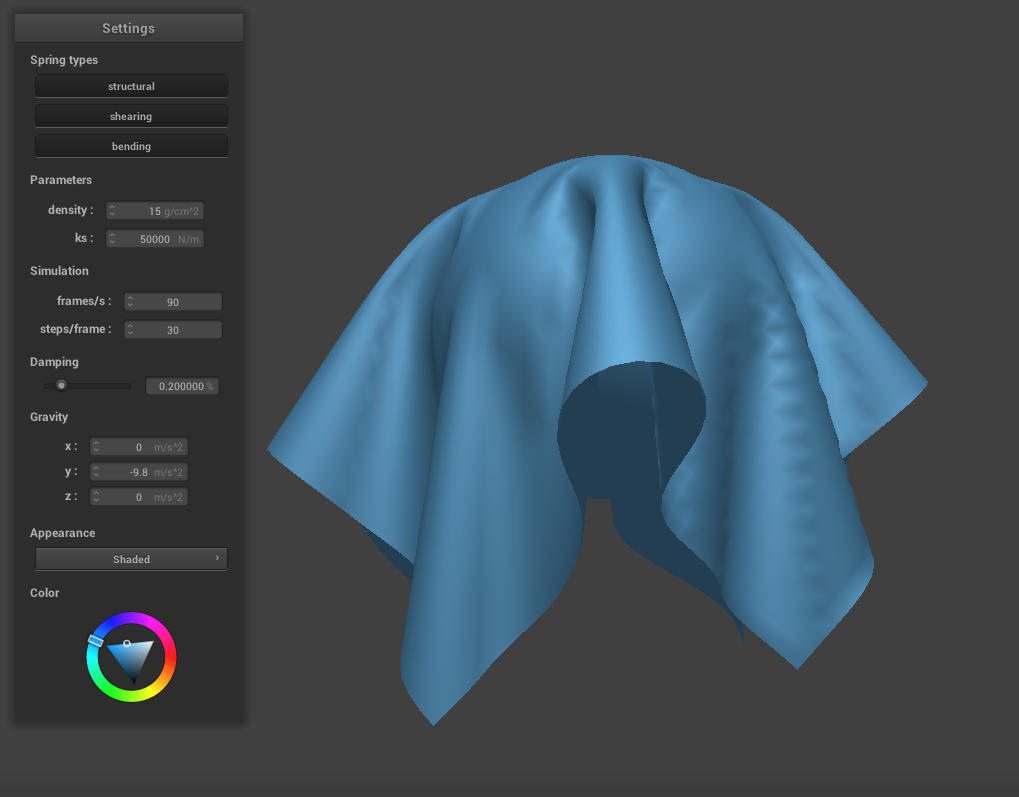
Similar to the previous part, adjusting the spring constant changes the cloth's appearance and behavior. If we lower ks to 500, the cloth appears thinner and drapes down the sphere more. The creases are also finer than with the default settings above. If we increase ks to 50000, the cloth becomes much stiffer. It appears thicker and heavier, and the folds are very large. These folds also begin at the very top of the sphere, whereas a lower ks produces folds that begin partway down.

Plane collision

The image below shows the cloth at it's resting state after falling onto the plane below it.

PART 4: SELF-COLLISIONS

We have handled collisions with other objects, but the cloth when the cloth collides with itself, it does not behave realistically. To fix this, we need to implement self-collisions. We will do so by partitioning th 3D space into 3D boxes with dimensions w * h * t, where w = 3 * width / num_width_points, h = 3 * height / num_height_points, and t = max(w,h). For each pointmass, we find which 3D box it falls into, and give it a unique number which corresponds to this box. Next, we fill in a hash table according to these values. We will map the unique floats we generated to a vector of all the point masses that fall in that box. Then, for each point mass, we check its distance to the other point masses in its box, using the hash table. For each of these point masses, if the distance from it to another in the list is less than 2 * thickness, we calculate the relevant correction vector. The final correction vector is the average of these pairwise correction vectors, scaled down by simulation_steps. The images below show how the cloth falls and folds on itself with default settings (k=5000, density=15)

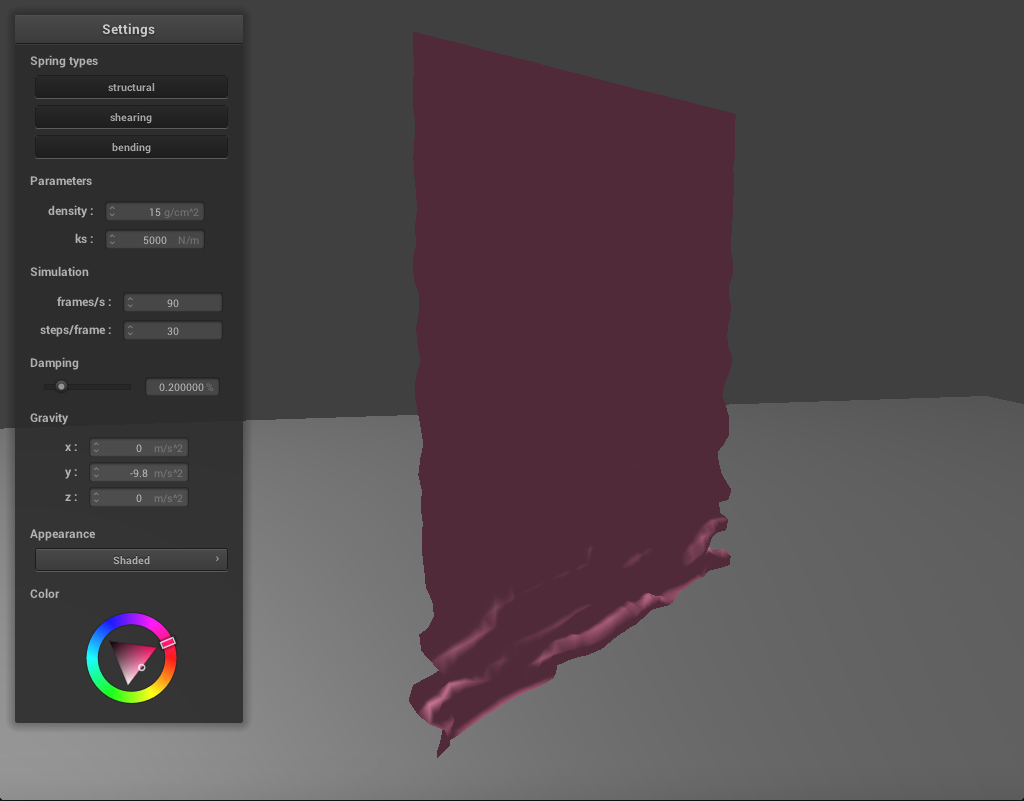
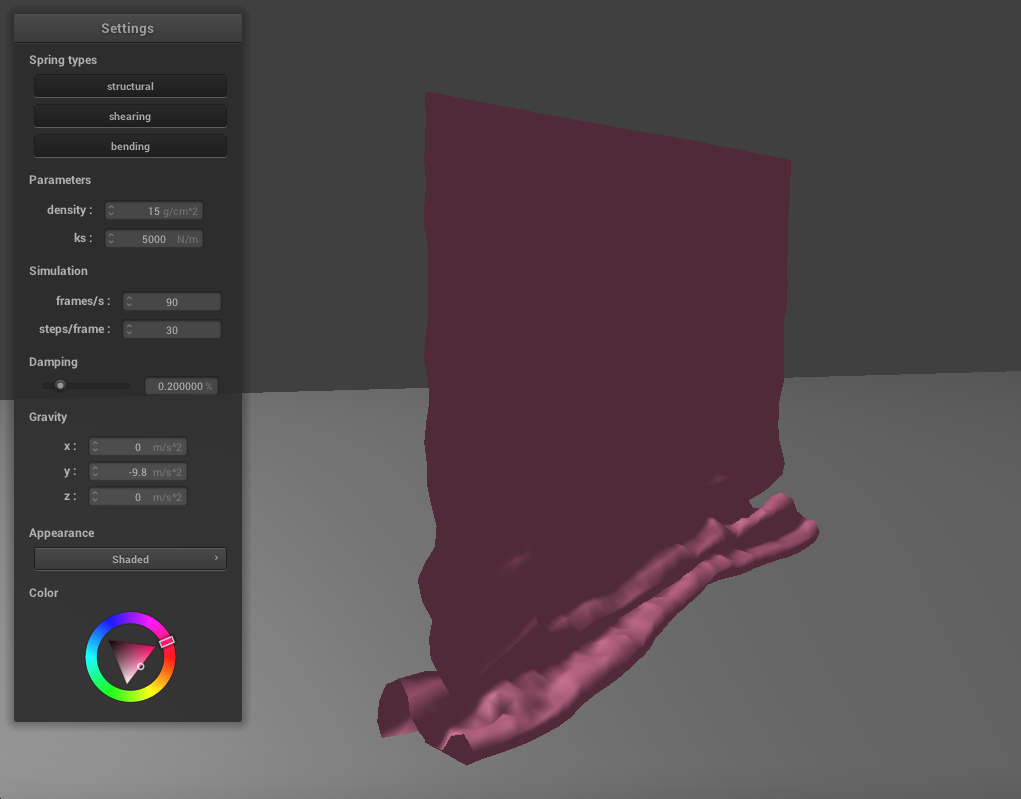
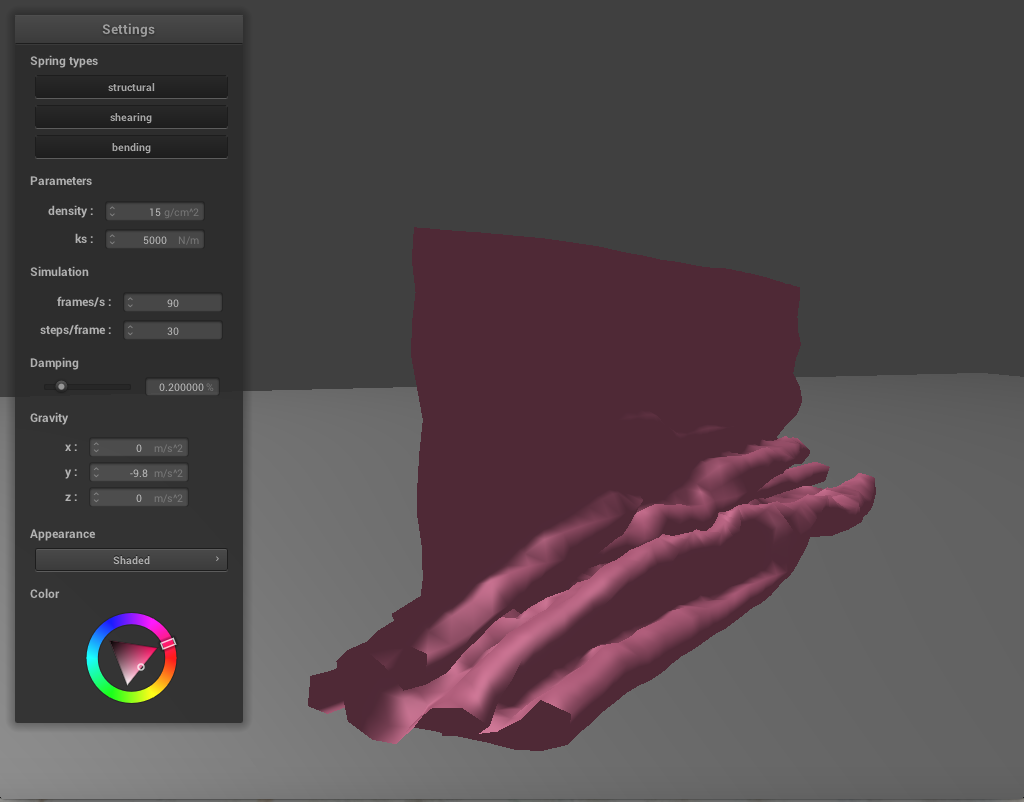
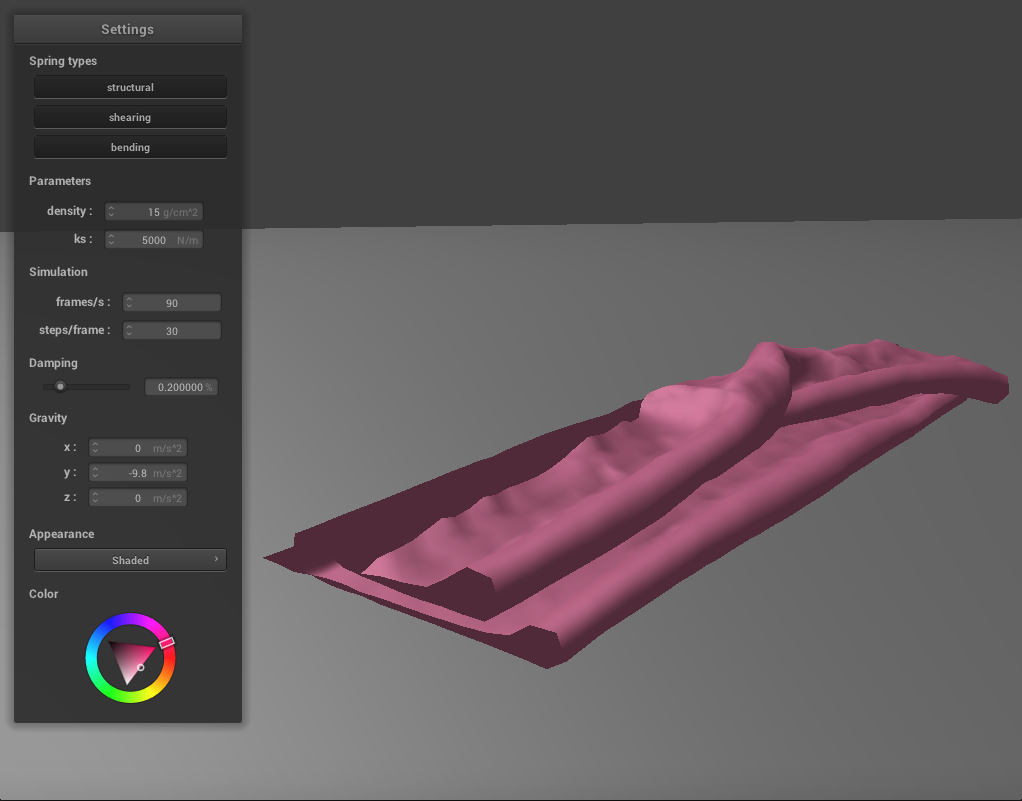
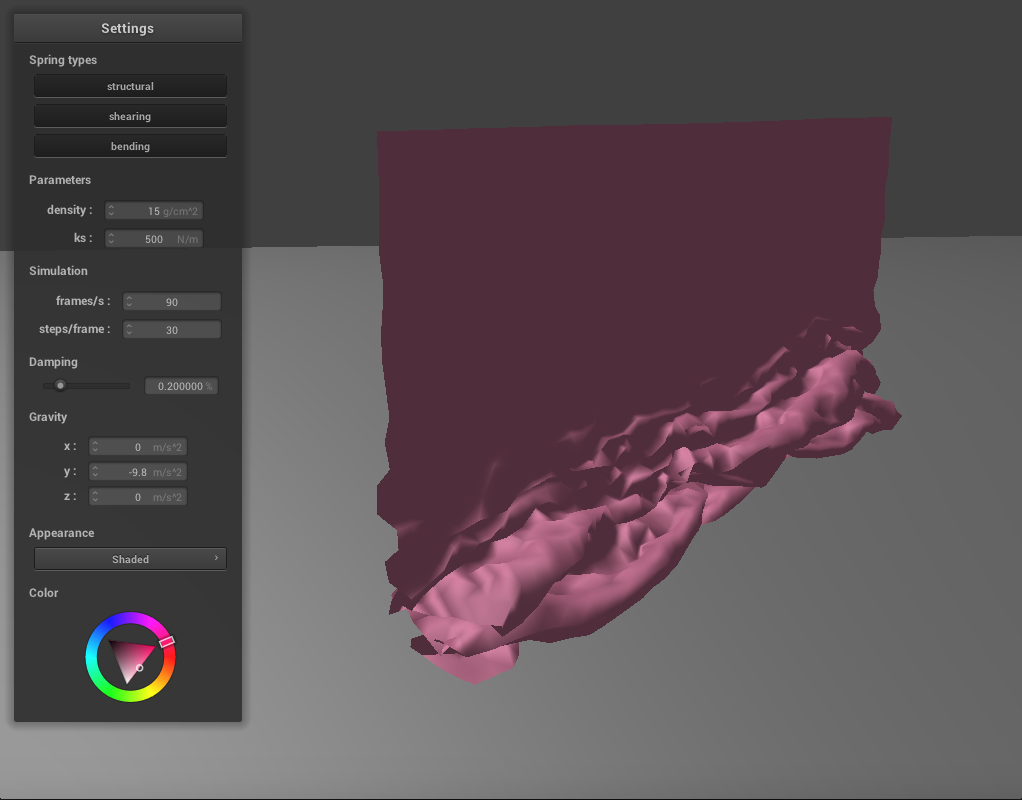
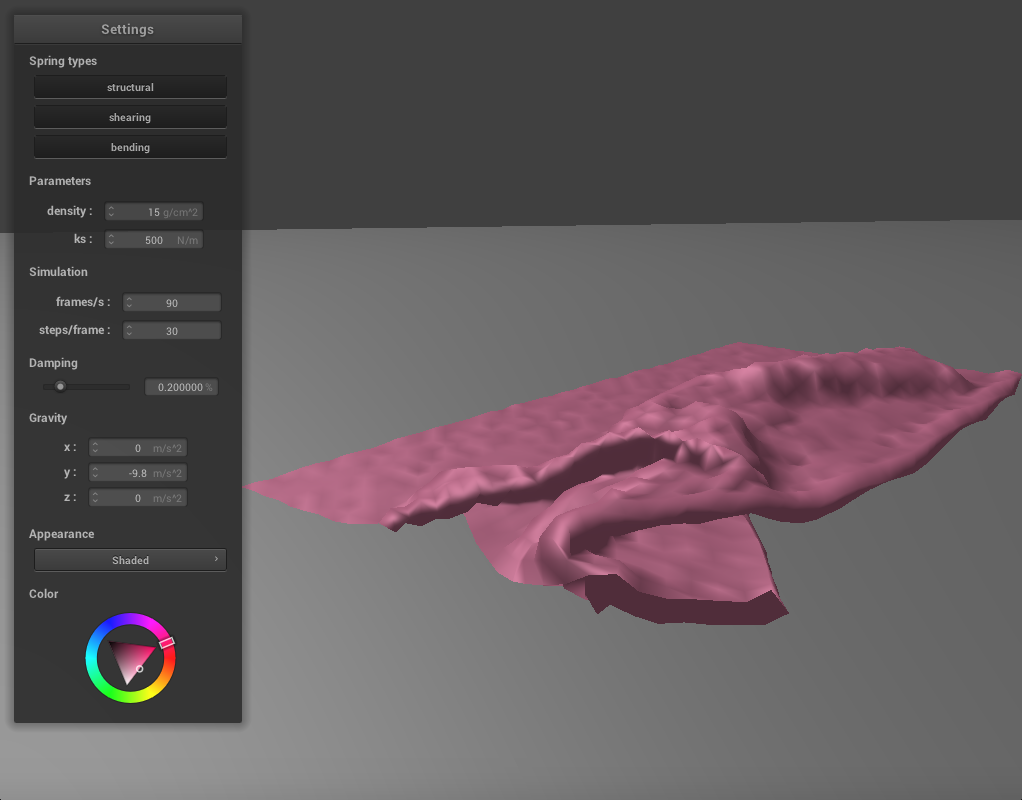
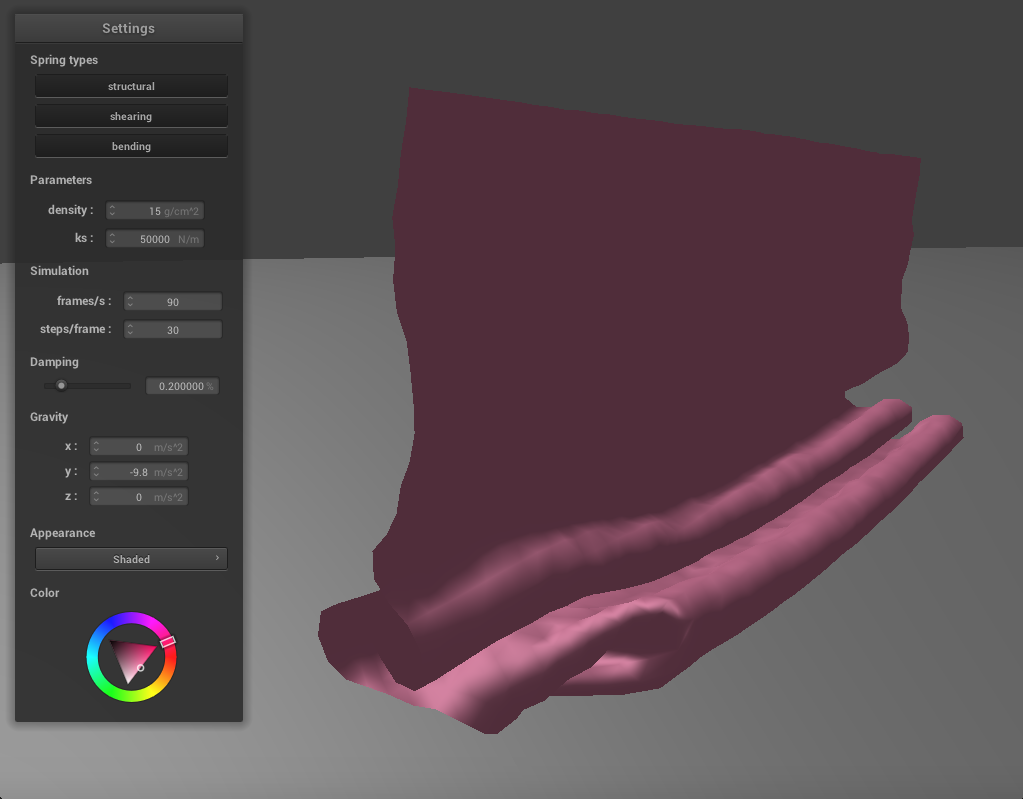
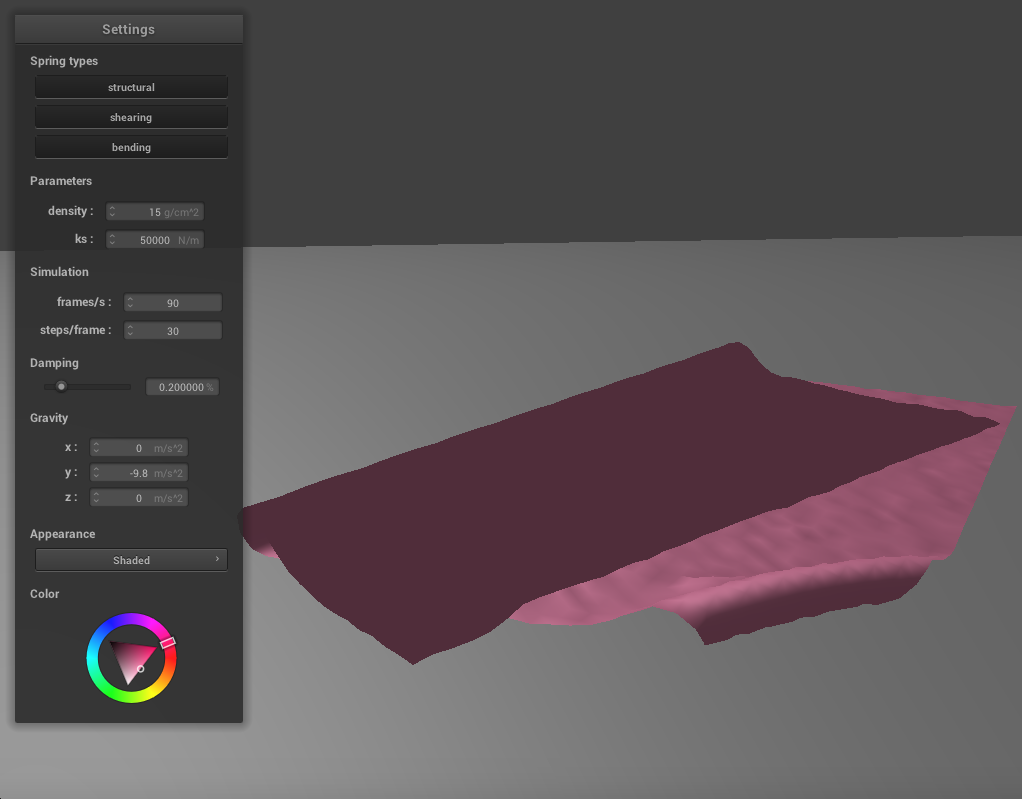
Varying the Spring Constant

We can adjust the spring constant as before to change how the cloth falls. If we reduce ks to 500, the cloth becomes much thinner and silk-like. There are a lot more folds as it falls and the creases are finer. In the final resting state, many of these folds are under the top part of the cloth, which folds at an angle. It takes some time for the cloth to come to a resting position where all the folds have settled, since there are so many. If we increase ks to 50000, the cloth becomes thicker and stiffer. It falls into very large folds with few creases, and in its final resting state it has essentially been folded in half. It also takes a while to reach this state as the springs keep adjusting until the corners have flattened out.

Varying Density

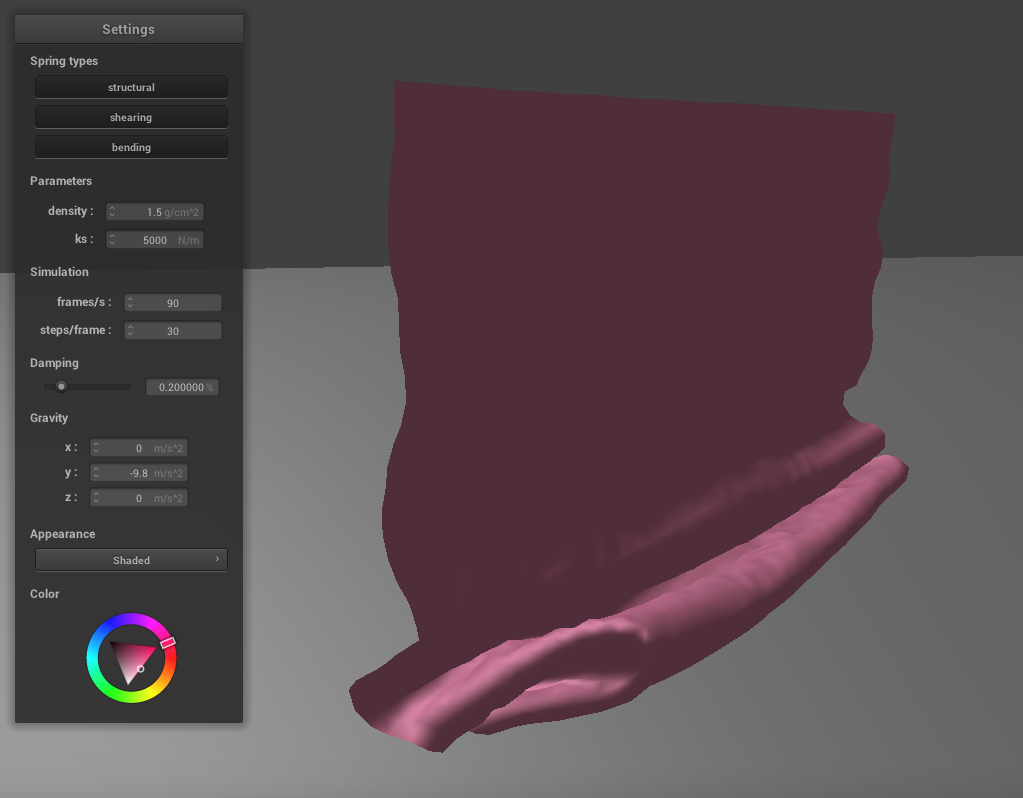
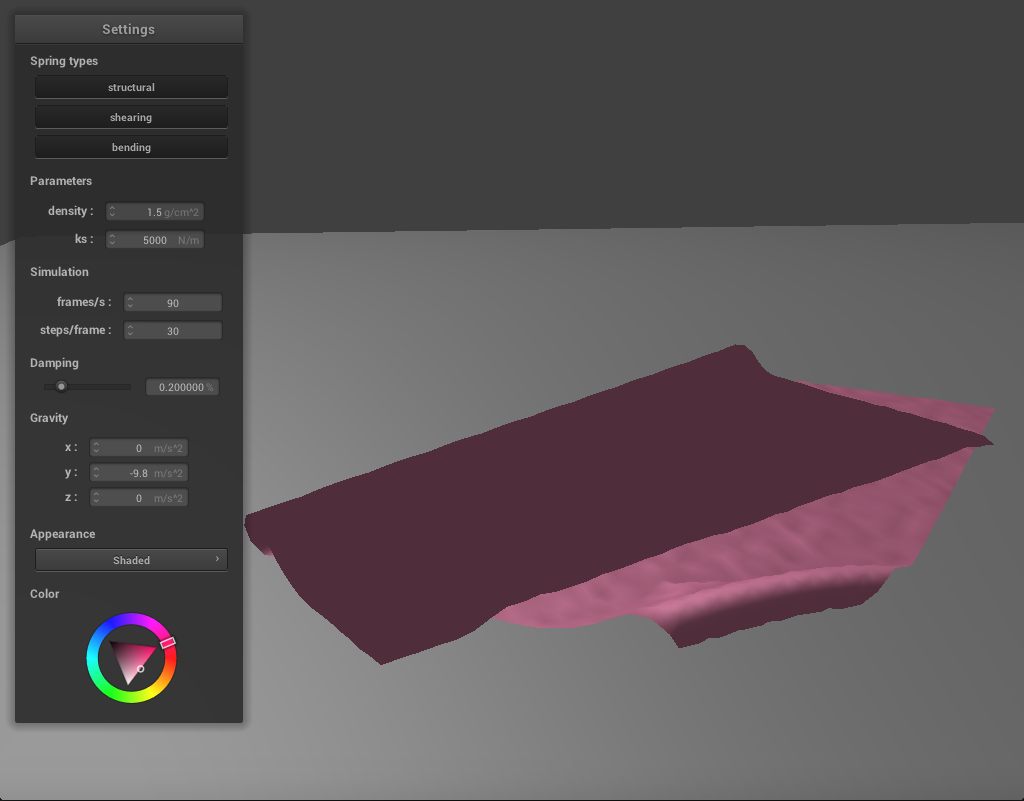
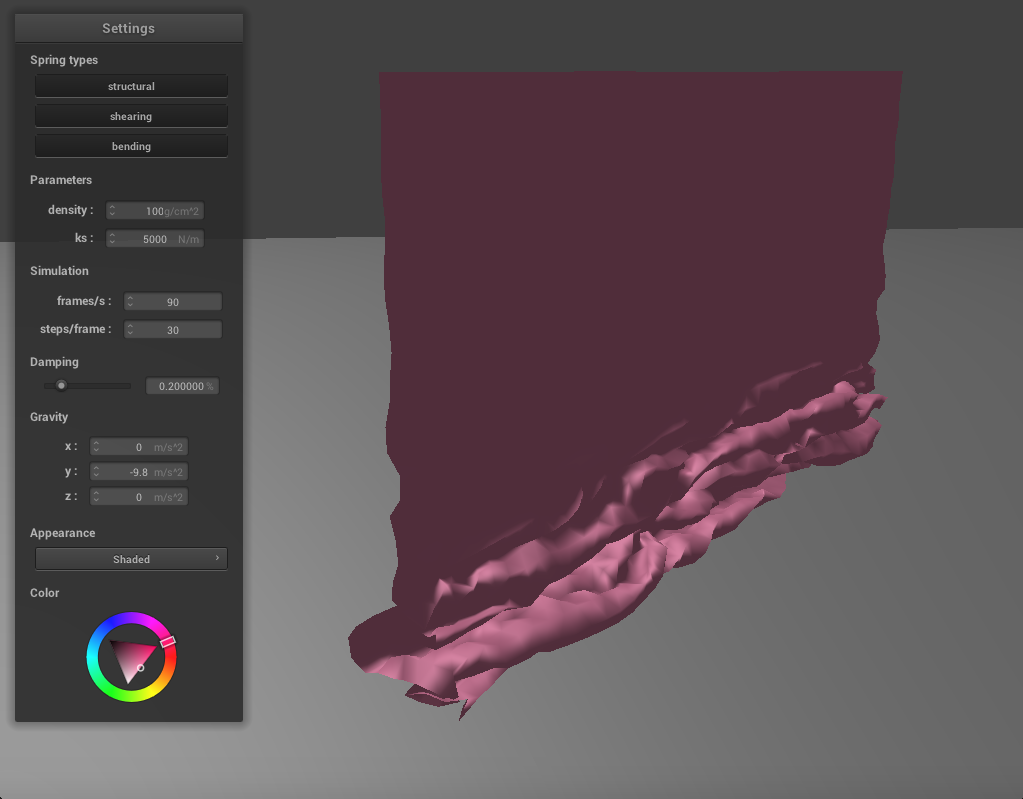
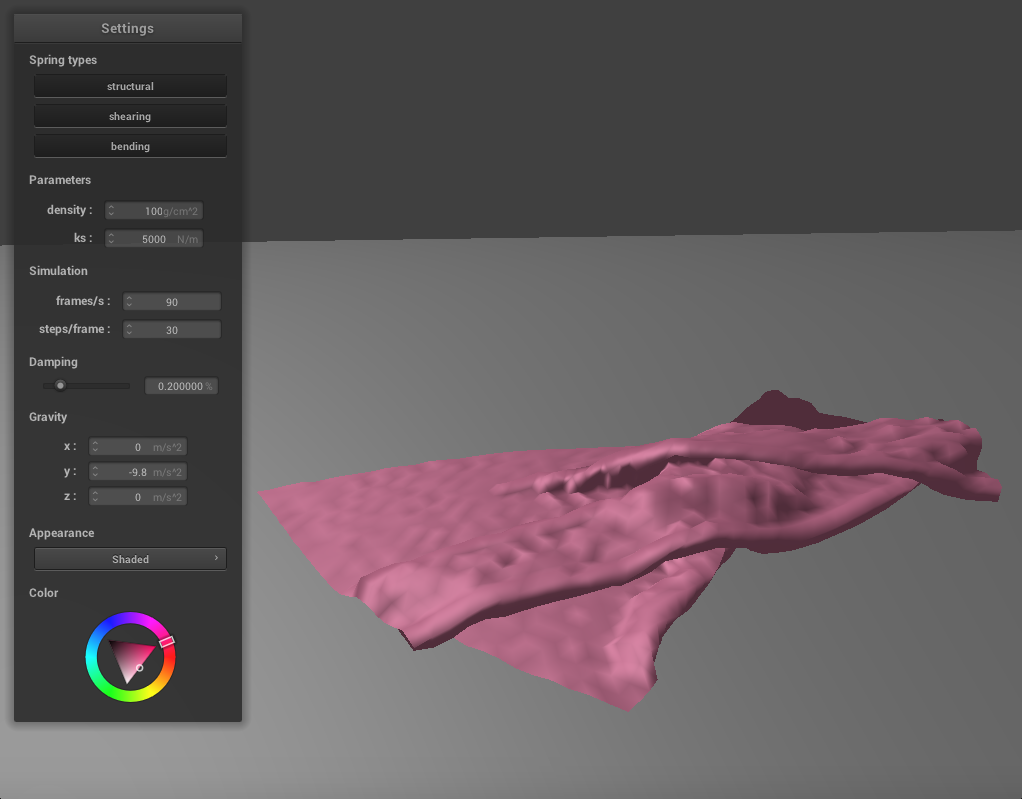
Again, we can also adjust the density to change how the cloth falls. If we lower the density, the cloth falls very similarly to the high ks example above. There are large folds, few creases, and the resting state shows the cloth folded in half. If we increase the density to 100, the cloth becomes much thinner, and behaves similarly to the low ks example above. There are many small folds and creases as it falls and the texture of the cloth appears silky.